





Ntokozo Magubane, Sudesh Sivarasu
ORCID ID: 0000-0001-6336-0669, 0000-0002-0812-568x
Division of Biomedical Engineering
Department of Human Biology
University of Cape Town
Western Cape
South Africa
Malebogo Ngoepe
ORCID ID: 0000-0002-3639-9063
Centre for Research in Computational and Applied Mechanics
Department of Mechanical Engineering
University of Cape Town
Western Cape
South Africa
Auto-injectors are medical devices used to inject medication into the intramuscular or subcutaneous layer of the body. They can be used for different disease applications such as anaphylaxis, rheumatoid arthritis, episodic migraines, multiple sclerosis, diabetes, and many others. This study focuses on developing a software application to size autoinjector components for different disease applications. The kinematic properties of an autoinjector are analysed and explained using a mathematical model that focuses on the plunger motion during the injection process. The mathematical model is validated by a physical experiment that uses a high-speed camera to capture the motion of the plunger during the injection process. The plunger displacement increases linearly during the injection process while the plunger velocity increases linearly and then reaches a constant velocity for the remainder of the injection process. The software application is developed using the validated mathematical model and optimising the relevant equations to determine the component dimensions of an auto injector.
Keywords: autoinjectors, IM injections, mathematical model
The autoinjector (AI) market is growing rapidly due the increasing demand for self-administration of medication and the growing prevalence of diseases that require intramuscular and subcutaneous injections (Global Industry Report, 2019–2026). Although AIs for some disease applications already exist, there is not an easy method to adapt these existing designs for other disease applications to meet market demand. Medications are injected into the intramuscular or subcutaneous layer for faster absorption as patients usually have limited time and minimal chances of survival during a shock. One of the biggest challenges in the auto-injector market is the increase in injectable natural drugs (Badkar et al, 2021). These drugs have complex formulations and concentrations, high viscosities and are prescribed in high dosages. For high viscosity drugs, a large spring force is needed to ensure an acceptably short injection time on the order of second (Zhong et al., 2020).
There are many models created to study the performance characteristics of an autoinjector, however none of the models are used to size autoinjector components. Predictions of injection time and injection force are important to ensure high preforming AIs. Injection time presents information on the variability of parameters in an auto-injector and is often calculated by considering the equilibrium of the static forces including stopper friction and pressure drop as described by the Hagen- Poiseuille equation (Thueer et al, 2018). This study aims to develop a medical device software to size autoinjector components and determine performance characteristics of autoinjectors for different disease applications.
The performance characteristics of an autoinjector were divided into three groups, namely kinematic properties, fluid properties and component dimensions. Table 1 shows the performance characteristics in their respective groups.
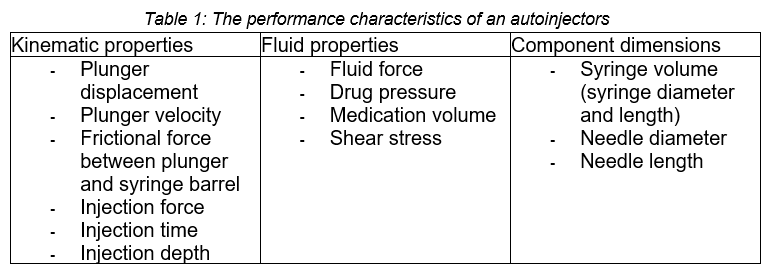
This study focuses on the kinematic properties and the component dimensions. A mathematical model was developed to explain the kinematic properties. The kinematic properties were analysed by considering the plunger inside an autoinjector and its motion. The forces that act on the plunger are 1) the spring force (because of the spring being compressed to force the plunger into motion), 2) the frictional force between the moving plunger and syringe and 3) the fluid resistance force as a result of the medication being injected into the patient.
The spring force (1) is defined as per Hooke’s law and depends on the displacement of the spring and the initial preload. The preload used was defined as 81 mm and the spring force reads:

The fluid force (2) is defined as the product of the drug pressure and syringe area. The drug pressure is a sum of the viscous pressure via the Hagen Poiseuille equation, the dynamic pressure losses via the Darcy Welsbach equation, the static pressure loss, and the pressure difference inside an auto-injector. The drug pressure is defined as:
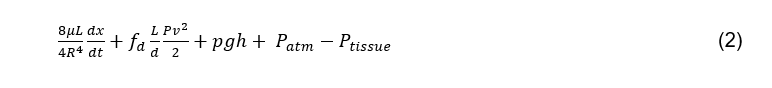
The frictional force (3) is equal to the product of static coefficient and the normal force when the plunger is stationary and the sum of the viscous and kinetic when the plunger is moving. The dynamic frictional force is:

The force acting on the plunger is coupled using force balance into a system of differential equations that are solved using MATLAB.
An experiment was conducted to validate the mathematical model. As part of this experiment, the spring properties were verified by compressing the spring and measuring the spring force and deflection using a Testometric force machine.
Two models were set up for the experiment:
A graphical user interface was used to determine autoinjector dimensions and performance characteristics. The software widgets are coded in Python Tkinter and functionality is based on the validated mathematical analysis conducted for this project. The user interface is validated using FDA software validation guidelines. These guidelines include (1) defining the software lifecycle as per the software life cycle for medical devices standard (IEC 62304); (2) defining the system requirements; (3) completing a risk register as per the risk management for medical devices standard (ISO 14971); (4) completing a design review at the end of the initial development phase to confirm that the system requirements are met; (5) conducting a traceability analysis to check how the source code compares to the design specification and ensuring that appropriate coding standards are adhered to.
There is a linear relationship between plunger displacement and time during the injection process. The results recorded are for water of viscosity 1 cP at 25℃. The displacement shown in Figure 1 below remains zero before actuation of the autoinjector and remains constant when the spring is fully compressed.
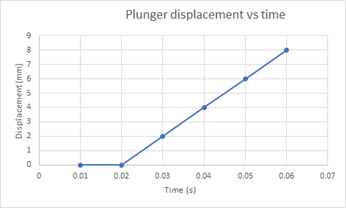
Figure 1: Plunger displacement vs time graph for water of viscosity 1cP at 25℃
The plunger velocity shown in Figure 2 increases linearly with time and reaches peak when the spring is fully compressed. The system rebounds between 0.03 to 0.04 seconds before reaching a constant velocity of 0.2 m/s. When the plunger is in contact with the fluid, the fluid pressure increases rapidly and reaches a constant pressure of 29.8 Pa. The numerical and experimental results agree with a percentage error of 4.25%. The discrepancy in the results is associated with the limited results recorded in the validation experiment and should be accounted for by analysing the fluid properties of an auto-injector. The syringe acceleration was not recorded in this study.
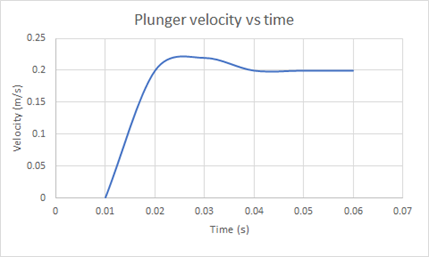
Figure 2: Plunger velocity vs time for water of viscosity 1cP at 25℃
The developed software allows a user to log in and define their user inputs. Thereafter, they can thereafter select the kind of analysis they would like to run, from (1) dimension; (2) injection force; (3) plunger displacement; (4) plunger velocity; (5) spring force (6) frictional force; (7) drug pressure and (7) fluid force.
The software authentication page is shown in Figure 3. The software:
Figure 3: Authentication page of the developed software.
This project focused on developing a graphical user interface using an experimentally validated mathematical model. The user interface is coded using Python Tkinter and validated using FDA software validation guidelines. The mathematical model developed in this study is based on the following assumptions: (1) the fluid is incompressible and Newtonian; (2) the flow is laminar through a syringe of constant circular cross-section; (3) the fluid is injected into a tissue of pressure 40 mmHg (5332 Pa). Further research is recommended to model the fluid properties using CFD.
I would like to extend my deepest gratitude to my supervisors, Prof Sudesh Sivarasu and A/Prof Malebogo Ngoepe for their support and guidance throughout this project. I would also like to thank the Impulse biomedical team for funding this project, offering their facility for the validation experiments and all their assistance during this study.
Auto-Injectors Market Size, Share, & Trends Analysis By Product Type (Disposable, Reusable), By Disease Indication (Rheumatoid Arthritis, Multiple Sclerosis, Diabetes, Anaphylaxis), By End Use (Homecare Settings, Hospitals & Clinics), And Segment Forecasts, 2019 - 2026. (2022). Retrieved 29 March 2022, from https://www.grandviewresearch.com/industry-analysis/auto-injectors-market
Wilkins, J., & Iain, S. (2012). Mathematical modeling for faster autoinjector design [Ebook] (12th ed., pp. 41-45).
Zhong, X., Guo, T., Vlachos, P., Veilleux, J., Shi, G., Collins, D., & Ardekani, A. (2021). An experimentally validated dynamic model for spring-driven autoinjectors. International Journal Of Pharmaceutics, 594, 120008. DOI:10.1016/j.ijpharm.2020.120008
Badkar, A. V., Gandhi, R. B., Davis, S. P., & Labarre, M. J. (2021). Subcutaneous delivery of high-dose/volume biologics: Current status and prospect for future advancements. Drug Design, Development and Therapy, 15, 159–170. DOI:10.2147/DDDT.S287323
Thueer, T., Birkhaeuer, L., & Reilly, D. (2018). Development of an advanced injection time model for an autoinjector. Medical Devices: Evidence and Research, 11, 215– 224. DOI:10.2147/MDER.S151727